Geometria analítica: Pontos

Plano cartesiano
   A geometria analítica teve como principal idealizador o filósofo francês René Descartes ( 1596-1650). Com o auxílio de um sistema de eixos associados a um plano, ele faz corresponder a cada ponto do plano um par ordenado e vice-versa.
   Quando os eixos desse sistemas são perpendiculares na origem, essa correspondência determina um sistema cartesiano ortogonal ( ou plano cartesiano). Assim, há uma reciprocidade entre o estudo da geometria ( ponto, reta, circunferência) e da Álgebra ( relações, equações etc.), podendo-se representar graficamente relações algébricas e expressar algebricamente representações gráficas.
   Observe o plano cartesiano nos quadros quadrantes:

    Exemplos:

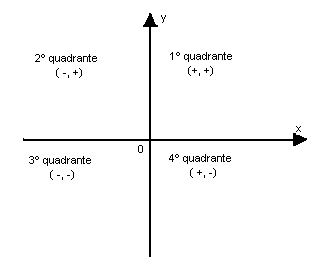
• A(2, 4) pertence ao 1º quadrante (x_A > 0 e y_A > 0)
• B(-3, -5) pertence ao 3º quadrante ( x_B < 0 e y_B < 0)

Observação: Por convenção, os pontos localizados sobre os eixos não estão em nenhum quadrante.

Distância entre dois pontos
   Dados os pontos A(x_A, y_A) e B(x_B, y_B) e sendo d_AB a distância entre eles, temos:

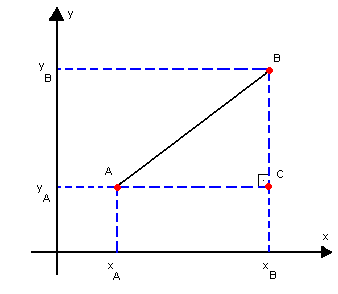   Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem:

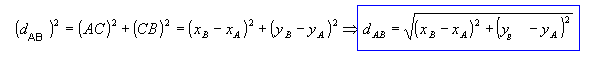
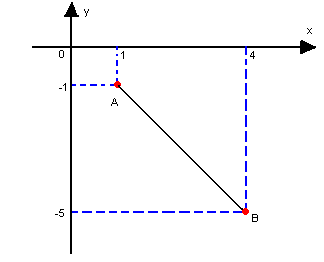
Como exemplo, vamos determinar a distância entre os pontos A(1, -1) e B(4, -5):

 

Razão de secção

   Dados os pontos A(x_A, y_A), B(x_B, y_B), C(x_C, y_C) de uma mesma reta 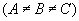, o ponto C divide 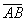numa determinada razão, denominada razão de secção e indicada por:

em que , pois se , então A = B.
   Observe a representação a seguir:

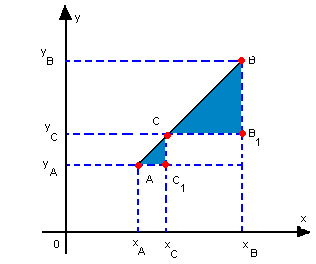
    Como o 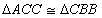, podemos escrever:

    Vejamos alguns exemplos:

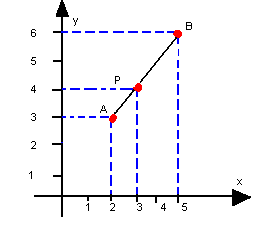
• Considerando os pontos A(2, 3), B(5, 6) e P(3, 4), a razão em que o ponto P divide é:

    Se calculássemos r_p usando as ordenadas dos pontos, obteríamos o mesmo resultado:

• Para os pontos A(2, 3), B(5, 6) e P(1, 2), temos:

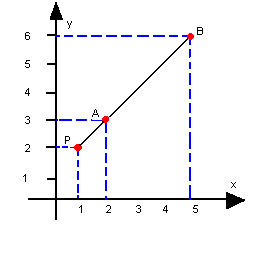   Assim, para um ponto P qualquer em relação a um segmento orientado contido em um eixo, temos:

• se P é interior a 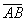, então r_p > 0  
• se P é exterior a 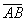, então r_p < 0
• se P = A, então r_p =0
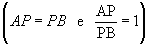
• se P = B, então não existe r_p (PB = 0)
• se P é o ponto médio de 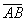, então r_p =1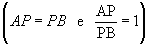
• Ponto médio
     Dados os pontos A(x_A, y_A), B(x_B, y_B) e P,  que divide 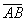ao meio, temos:
  Assim: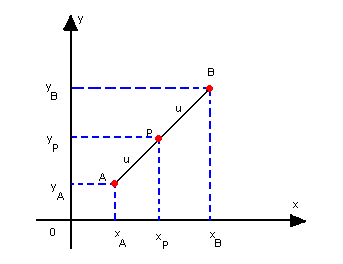
  
  
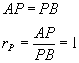
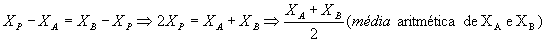
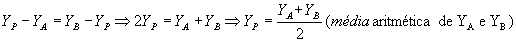
  Logo, as coordenadas do ponto médio são dadas por:
  
  
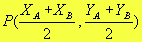  Baricentro de um triângulo
     Observe o triângulo da figura a seguir, em que M, N e P são os pontos médios dos lados 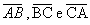, respectivamente. Portanto, 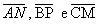são as medianas desse triângulo:
  
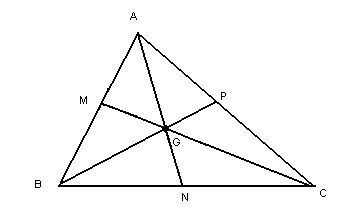      Chamamos de baricentro (G) o ponto de intersecção das medianas de um triângulo.
     Esse ponto divide a mediana relativa a um lado em duas partes: a que vai do vértice até o baricentro tem o dobro da mediana da que vai do baricentro até o ponto médio do lado.
  Veja: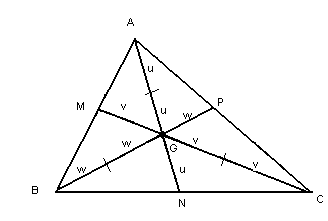
   
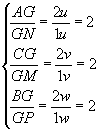  Cálculo das coordenadas do baricentro
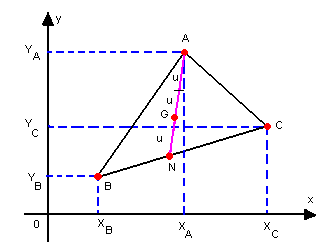
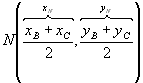     Sendo A(X_A, Y_A), B(X_B, Y_B) e C(X_C, Y_C) vértices de um triângulo, se N é ponto médio de , temos:
  Mas: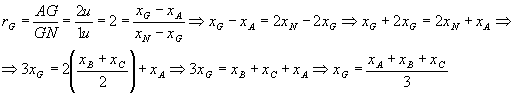
  
  Analogamente, determinamos 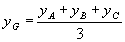. Assim: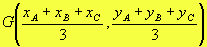
  
  
• Condições de alinhamento de três pontos
     Se três pontos, A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C), estão alinhados, então:
  
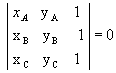              Para demonstrar esse teorema podemos considerar três casos:
  a) três pontos alinhados horizontalmente
  
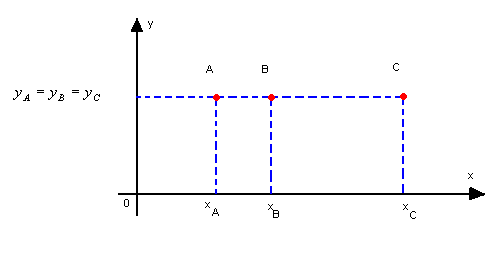      Neste caso, as ordenadas são iguais:
  y_A = y_B = y_C
  e o determinante é nulo, pois a 2ª e a 3ª coluna são proporcionais.
  b) três pontos alinhados verticalmente
  
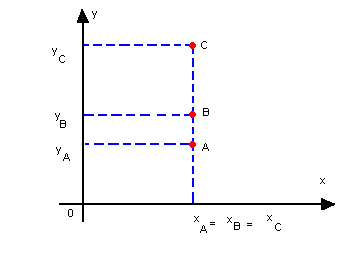      Neste caso, as abscissas são iguais:
  x_A = x_B = x_C
   e o determinante é nulo, pois a 1ª e a 3ª coluna são proporcionais.
  c) três pontos numa reta não-paralela aos eixos
  
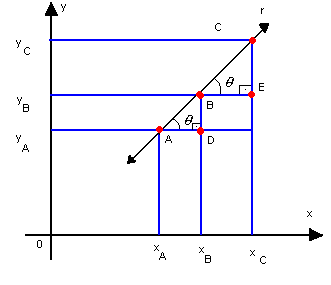  Pela figura, verificamos que os triângulos ABD e BCE são semelhantes. Então:
  
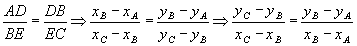  Desenvolvendo, vem:
  
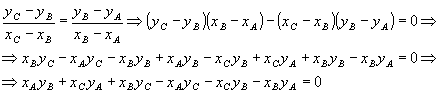  Com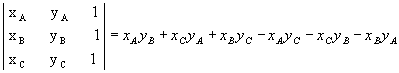o:
  
  então .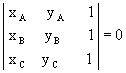
  Observação: A recíproca da afirmação demonstrada é válida, ou seja, se 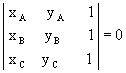, então os pontos A(x_A,y_A), B(x_B,y_B) e C(x_C, y_C) estão alinhados.